FELIZ AÑO NUEVO

Preparación examen opción C

Simulacro de examen de toma de imágenes (con solución)

Simulacro opción C: fibra óptica (con solución)

IB Examen Opción C Toma de muestras curso 2017-2018

Examen Toma de muestras (con solución) curso 2018-2019

Examen lente (Convexa) /telescopio (con solución) curso 2018-2019

Examen fibra óptica (con solución) curso 2018-2019

Examen fibra óptica curso 2019-2020

Examen óptica geométrica nacional curso 2019-2020

Examen toma de imágenes e instrumentos curso 2019-2020

Examen óptica geométrica nacional Solución curso 2022-2023

PRISMA ÓPTICO

Desviación angular de prismas

El ángulo del prisma (A) es igual a la suma de los ángulos Theta prima.

DESCOMPOSICIÓN DE LA LUZ BLANCA

Descartes explicó la formación del arco iris y años más tarde Newton estudió la luz y logró descomponerla en los colores de su espectro por medio de un prisma - año1666-.

Newton sabía muy poco sobre la naturaleza de la luz, no sabía que era una onda y menos aún que era una onda electromagnética. Creía que estaba formada por corpúsculos, pero consiguió descomponerla en sus colores espectrales. Hoy sabemos que la luz es a la vez partícula y onda.

Los seres humanos (y algunos animales) apreciamos una amplia gama de colores que, por lo general, se deben a la mezcla de radiaciones (luces) de diferentes longitudes de onda. El color de la luz con una única longitud de onda o una banda estrecha de ellas se conoce como color puro.

Al hacer pasar la luz por un prisma de cristal, las distintas longitudes de onda que componen el haz de luz viajan dentro de él a diferente velocidad y se curvan de manera diferente al entrar y al salir (doble refracción al cambiar de medio) dando como resultado un haz desviado de la dirección inicial y con sus componentes separados. Así surge el espectro solar.

Cada uno de los diferentes rayos de luz atraviesa el cristal con distinta velocidad y la velocidad media de la luz dentro del prisma es menor que en el vacío. La luz es una onda con un campo eléctrico oscilante que interfiere con la partículas cargadas que hay en la materia.

Cómo puedes observar en la imagen inicial de esta página, siempre que la luz incide en una cara se refleja y se refracta al mismo tiempo. 

Las radiaciones visibles están comprendidas entre las siguientes longitudes de onda: desde 350 nm (nanómetros) para el color violeta hasta 750 nm para el rojo.

Las gotas de agua suspendidas en la atmósfera también descomponen la luz y forman el arco iris.

Con ayuda de un prisma podemos analizar la luz blanca y los colores emitidos por los diferentes elementos: Na, C, He, etc. Podemos identificar y distinguir los elemento por los colores que emiten. Cada elemento tiene unos niveles energéticos permitidos por los que circulan los electrones. Los saltos entre estos niveles son los que dan los tipos de radiaciones -los colores- que lo identifican. Cada elemento tiene un espectro característico.

A continuación vemos las rayas de color emitidas por el carbono (el espectro del C):

El sodio (metal muy reactivo) emite una luz amarilla. Las lámparas que iluminan las carreteras son algunas veces de vapor de sodio. Los coches llevan luces emitidas por gases halógenos (son muy luminosas).

FIBRA ÓPTICA

FIBRA ÓPTICA

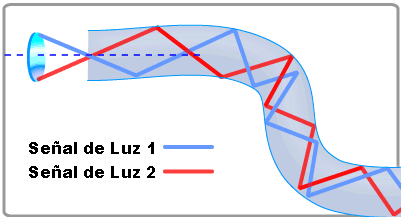
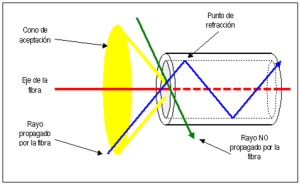
Las fibras ópticas funcionan gracias al principio de la reflexión total interna, ver Fig. 01, que se da debido a que la fibra o núcleo tiene un cierto índice de refracción superado por el del revestimiento, por lo tanto el rayo de luz, cuando se “desplaza” por la fibra y choca con la pared de ésta, se produce el mismo efecto que observan los buzos cuando están debajo del agua; éstos, cuando ven hacia arriba hacia la superficie del agua, pueden ver lo que está afuera pero sólo hasta cierto ángulo de la vertical, a partir de este ángulo sólo verán un reflejo de lo que esta alrededor de ellos; eso mismo pasa en la fibra, como si ésta fuera el agua, y el revestimiento el aire más arriba de la superficie, que tiene menor índice de refracción.

Los rayos de luz pueden entrar a la fibra óptica si el rayo se halla contenido dentro de un cierto ángulo denominado cono de aceptación. Un rayo de luz puede perfectamente no ser transportado por la fibra óptica si no cumple con el requisito del cono de aceptación. El cono de aceptación está directamente asociado a los materiales con los cuales la fibra óptica ha sido construida. La siguiente figura 02 ilustra todo lo dicho:

En el siguiente vídeo se puede ver ¿Cómo funciona la fibra óptica?

DETERMINACIÓN DE LA VISCOSIDAD DE UN FLUIDO DESCONOCIDO (LEY DE STOKES)

ESTUDIO DEL MOVIMIENTO (m.r.u)

Introducción

Una partícula cuando desciende en el seno de un fluido está sometida a un conjunto de fuerzas. En la dirección del movimiento actúa el peso de la partícula y en dirección contraria el empuje del fluido y el rozamiento de la partícula con el fluido.

Desde el momento en que se inicia el movimiento dentro del fluido hay dos fases:

• Durante la primera fase, la fuerza resultante es positiva en el sentido de avance de la partícula, y por tanto, se produce un movimiento acelerado que incrementa paulatinamente la velocidad de la partícula.
• Al aumentar la velocidad también lo hace la fuerza resistente o rozamiento, hasta que llega un momento en el que las fuerzas se anulan y la aceleración se hace cero, alcanzándose en ese instante la velocidad máxima. A partir de se momento se desarrolla una segunda fase, que se caracteriza por que la velocidad se mantiene constante en el valor máximo alcanzado. esta velocidad es conocida con el nombre de velocidad terminal o límite, v.

En la práctica esta segunda fase es la importante, ya que la primera es muy corta y apenas influye en el experimento. Para estudiar la velocidad límite y la viscosidad de un determinado medio, se recurre al enunciado de Stokes. La Ley de Stokes se refiere a la fuerza de fricción experimentada por objetos esféricos moviéndose en el seno de un fluido viscoso en un régimen laminar de bajos números de Reynolds. Fue derivada en 1851 por George Gabriel Stokes. En general la ley de Stokes es válida en el movimiento de partículas esféricas pequeñas moviéndose a velocidades bajas.  Base física para la determinación de la viscosidad de un fluido desconocido (Ley de Stokes)

Esta ecuación se cumple siempre que el movimiento de la partícula no sea muy elevado y provoque turbulencias dentro del fluido, momento en el cual la resistencia no sigue la ley de Stokes.

En esta práctica, una serie de variables son constantes: densidad del detergente (1,020 g/ml), gravedad (9,81 m/s2) y densidad de la canica (2,450 g/ml)

Objetivos

• Estudiar el movimiento producido al caer una bola por un líquido viscoso
• Determinar la viscosidad del fluido desconocido.

Procedimientos

Vamos a analizar como se mueve una bola de cristal cuando se la deja caer en el interior de detergente y medir esa velocidad límite de forma experimental, para ello preparamos un tubo de metacrilato con detergente y realizamos marcas espaciadas en él para poder tomarlas como referencia. Por lo expuesto anteriormente debemos dejar un espacio entre la parte alta del detergente y la primera marca en el cual la bola adquiere la velocidad constante de caída en el seno del fluido.

En este caso vamos a tirar 5 canicas de distintos radios, de tal forma, que el radio es la variable dependiente y la velocidad es la variable dependiente, y nuestra incógnita es la viscosidad del detergente.

Materiales

• Tubo de metacrilato
• Bolas de vidrio
• Detergente
• Regla
• Cronómetro
• Calibre*

* El siguiente GIF animado (obra de Joaquim Alves) te ayudará con el funcionamiento de calibre.

Densidad de los sólidos: balanza Jolly

Determinación de la densidad de los sólidos: la balanza  Jolly

Consiste en determinar la densidad de un objeto sólido aplicando las leyes de Hooke, segunda ley de Newton y el principio de Arquímedes.

La balanza de Jolly, consiste en un resorte vertical, cuyo extremo superior está en

contacto con un punto fijo y cuyo extremo inferior está en contacto con el objeto cuya

densidad se quiere averiguar y que este mismo, por la acción de su peso deforma el

resorte una longitud X1.

Luego el mismo, objeto colgante toma contacto con el agua y como oposición de la

fuerza de empuje, el resorte se deforma una longitud X2, menor a la anterior, como

se muestra en la figura B1.

Si colgamos una masa y determinamos el alargamiento en el aire (X1) y en el agua (X2), a partir de la siguiente ecuación:


densidad experimental= densidad agua*(X1/(X1-X2))  (base física de la balanza Jolly)

Determinación de K: método dinámico

DETERMINACIÓN DE K: Método dinámico.

En la determinación de la constante elástica de un resorte por el método dinámico, lo que hacemos es dejar oscilar el resorte y medir su periodo de oscilación.

Deducción de la ecuación del periodo del muelle elástico

Si colgamos distintas masas de un resorte y tiramos de ellas separándolas de su posición de equilibrio, al soltarlas oscilan con distintos periodos. Medimos los periodos del resorte para distintas masas oscilantes (teniendo en cuenta la masa del portapesas). No importa si estiramos más o menos antes de soltarlas. A partir de la relación de la masa y del periodo de oscilación podemos hallar la constante del resorte.

Cuelga del resorte diferentes masas conocidas.
Para cada una de ellas realiza la experiencia lanzando el resorte y midiendo el tiempo que emplea en dar 20 oscilaciones completas (desprecia las dos o tres primeras).
Halla el período de una oscilación y registra los datos en una tabla como la siguiente:

Medidas	m (kg)	t (s)	T (s)	T2 (s2)	k (N/m)	D k
1ª
2ª
3ª
4ª
5ª
					km=

La dispersión de los datos te indicará cuantas medidas realizar.

Tratamiento de datos

1.- Tratamiento analítico
Determina en cada caso el valor de k aplicando la fórmula:

K = 4    p² m / T ²

Determina el valor medio de la constante k (media aritmética) y toma k_m como valor verdadero.
Calcula las desviaciones absolutas ∆k, así como la desviación absoluta media ∆km.
Expresa el resultado de la medida como: km ± ∆km



2.-Tratamiento gráfico 

Realiza la gráfica con las indicaciones que dispones:

Partiendo de los datos anteriores representamos T2 en ordenadas frente a la masa en abscisas. Los puntos obtenidos no caen exactamente sobre una recta, pero nosotros trazaremos una que se aproxime lo más posible a todos ellos logrando que la distancia de todos ellos respecto a esa recta ideal sea la menor posible (mínima). En esto consiste el ajuste de la recta por el método de mínimos cuadrados.

Con este enlace al programa de mínimos cuadrados) puedes hallar la recta que se ajusta a los puntos que obtienes en la práctica. El programa te da la pendiente de la recta.

Pendiente = D T ² / D m = (4 p ²) / k

El valor de la pendiente es "m" en la gráfica que verás en el programa.

Una vez conocida la pendiente, la igualamos a (4 p²) / k y hallamos K.

Al pasar la recta por el medio de los puntos obtenidos se promedian los valores (se halla su media gráficamente).

DEFINICIÓN NUEVA DEL KILOGRAMO

DEFINICIÓN NUEVA DEL KILOGRAMO

Un kilo de naranjas, de azúcar o de polvorones, pesa, por definición, lo mismo que el cilindro de platino-iridio guardado bajo varias campanas protectoras y encerrado con tres llaves en el sótano del Pabellón de Breteuil a las afueras de París. Este Prototipo de Kilogramo Internacional (IPK), empleado para calibrar los patrones oficiales de la unidad de masa, anuncia este viernes su jubilación tras 129 años de servicio. En la última sesión de la vigésimosexta Conferencia General de Pesos y Medidas celebrada este viernes en Versalles, los 60 Estados miembros han votado de forma unánime a favor de redefinir el kilogramo: a partir del año que viene, la unidad de masa no será un objeto físico, sino un valor derivado de una constante de la naturaleza. Este cambio no tendrá ninguna implicación en la cesta de la compra ni se notará en el día a día, pero puede ser muy importante en ámbitos científicos como el desarrollo de medicinas.

MÁS INFORMACIÓN

• 

  La batalla científica para que un kilo siempre sea un kilo

“Se está haciendo historia de la ciencia. Esto se contará en los libros de texto”, ha dicho José Manuel Bernabé, director del Centro Español de Metrología y delegado de España en la conferencia. Los metrólogos reunidos, expertos en el campo de la medición de magnitudes, llevan años preparando el cambio al Sistema Internacional de Unidades, que incluirá redefiniciones del mol, del kelvin y del amperio para que estas unidades también se basen en constantes universales.

El kilogramo recibe especial atención por ser la última unidad fundamental cuya definición todavía depende de la magnitud de un objeto físico. Y eso es un problema, señalan los científicos, porque el objeto no es inmutable. En el último siglo, la masa del IPK ha fluctuado. Sigue siendo un kilo, ya que por convenio no puede haber incertidumbre en su valor, pero con respecto a la masa de otros patrones del kilo, ha variado por valores de al menos 50 microgramos (millonésimas del gramo). Esto es porque el cilindro se puede ensuciar con partículas del aire y pierde pequeñas cantidades de material cuando se limpia.

“Sentimos, sobre todo, alivio de que la decisión esté tomada”, dice Stuart Davidson, jefe de metrología de masa en el laboratorio físico nacional (NPL) de Reino Unido, uno de los centros más involucrados en la redefinición del kilogramo

Los microgramos no afectan a la compra de fruta o de polvorones, pero sí se deben tener en cuenta durante la síntesis de nuevos fármacos, por ejemplo. En la investigación física, tales fluctuaciones son “intolerables”. Según explica Bernabé, con esta decisión “se están poniendo los cimientos para la nueva ciencia, una con menos incertidumbre para el desarrollo de la tecnología”.

“Sentimos, sobre todo, alivio de que la decisión esté tomada”, dice Stuart Davidson, jefe de metrología de masa en el laboratorio físico nacional (NPL) de Reino Unido, uno de los centros más involucrados en la redefinición del kilogramo. “Hay gente que lleva trabajando en esto toda su vida profesional. Ahora podemos centrarnos en mejorar la tecnología y la precisión de nuestras mediciones”, añade.

Otro incentivo para retirar el IPK ha sido el peligro de que el cilindro resulte dañado o se deforme. El metro, que solía ser la longitud de una barra de platino, ya se redefinió en 1983 precisamente para evitar estos problemas. Al fijar la velocidad de la luz —constante en el vacío— con un valor numérico universal, los metrólogos acordaron llamar al metro “la distancia que viaja la luz en 1/299.792.458 segundos”. Cualquier laboratorio capaz de medir el paso del tiempo con precisión puede calibrar su propia barra de metro.

Revolución en la medición

El valor del kilogramo se derivará de la constante de Planck gracias a una balanza de potencia

Con el kilogramo ocurrirá lo mismo, cuando los cambios aprobados entren en efecto el 20 de mayo de 2019, el aniversario del Tratado del Metro de 1875. "El 20 de mayo de 2019 se vivirá la mayor revolución en la medición desde la Revolución Francesa", aseguró el premio Nobel Bill Phillips desde el escenario. En lugar de la velocidad de la luz, la cifra inmóvil elegida para definir la unidad de masa es la constante de Planck, un valor que describe los paquetes de energía emitidos en forma de radiación. La aprobación de esta definición del kilogramo ha tardado años en llegar porque hasta hace poco no existían los medios tecnológicos para llevarla a la práctica. Ahora, gracias a un aparato llamado la balanza de Watt (a veces balanza de Kibble o balanza de potencia), se pueden calibrar patrones del kilo conocido el valor de la constante de Planck.

FUENTE: El País