GRÁFICAS DEL CAMPO GRAVITATORIO

Las anteriores no son las únicas gráficas que verás relacionadas con los campos gravitatorios. Aquí señalamos algunas de las más comunes:

Gráfica de energía potencial en función de la distancia

En esta gráfica se suele representar la distancia al origen ( r ) en el eje x, y el valor de la energía potencial gravitatoria ( Ep ) en el eje y. Normalmente verás está gráfica asociada a la energía potencial gravitatoria Ep(r)que posee una masa m ( puntual o esférica de radio R ) en presencia de otra masa M. Recuerda que, en ese caso, Ep(r)=−G⋅m⋅Mr  .

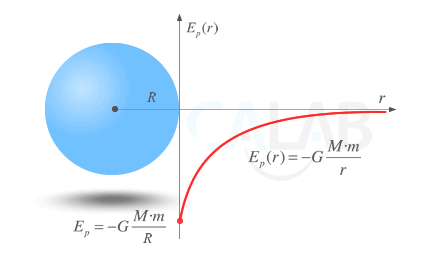
Energía potencial gravitatoria

La energía potencial gravitatoria que adquiere un cuerpo de masa m debido a la presencia de una masa M varía de forma inversamente proporcional a la distancia al cuerpo generador de campo y es negativa, siendo su valor cero en el infinito.

Estas gráficas son particularmente útiles para estudiar la órbita de un planeta a partir de su energía.

Gráfica de potencial gravitatorio en función de la distancia

En esta gráfica se suele representar la distancia al origen ( r ) en el eje x y el valor del potencial gravitatorio ( V) en el eje y. Normalmente también la encontrarás asociada al potencial gravitatorio que produce un cuerpo ( puntual o esférico de radio R ), de masa M a una determinada distancia r y es prácticamente igual a la anterior, salvo que no tiene en cuenta la masa m sobre la que actúa, al ser el potencial la energía potencial por unidad de masa. Recuerda que, en ese caso, V(r)=−G⋅Mr  .

Potencial Gravitatorio

El potencial gravitatorio que genera un cuerpo de masa M en un punto es inversamente proporcional a la distancia entre el punto y el cuerpo considerados. Su valor es negativo, creciendo a medida que nos alejamos y haciéndose 0 en el infinito.

Observa que el valor del potencial a una determinada distancia ri se puede asociar a la superficie equipotencial que se encuentre a dicha distancia.

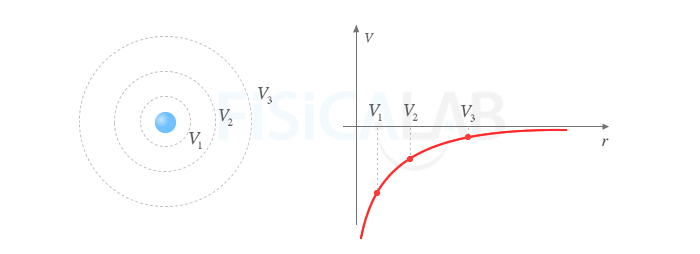
Gráfica del potencial gravitatorio en base a sus superficies equipotenciales

En el caso del potencial creado por masas puntuales o masas esféricas en su exterior, el valor asociado a cada superficie equipotencial depende del radio de esta, es decir, de la distancia de la superficie al cuerpo.

Podemos tener una versión tridimensional de esta gráfica si, en lugar del eje r consideramos un plano. Asociaremos a cada punto del plano, situado a una determinada distancia r del origen donde se sitúa el cuerpo, un valor de potencial gravitatorio sobre el eje z, tal y como se aprecia en la figura.

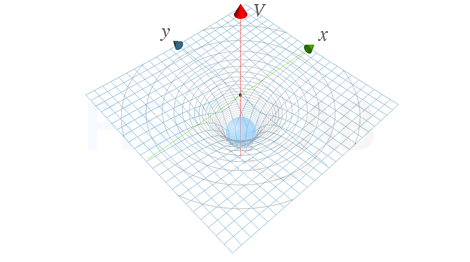
Potencial Gravitatorio en 3D

Los puntos del plano OXY, representan la distancia del punto real al cuerpo generador de campo. Sobre el eje z se representa el valor concreto del potencial gravitatorio para esa distancia r. La unión de todos los valores de dicho potencial se representan mediante la malla de la figura.

Las lineas concéntricas grises sobre la malla representan valores específicos de potencial asociados a tales distancias y se relacionan directamente con las superficies equipotenciales.

Observa que para distancias muy próximas al cuerpo,en la superficie del mismo, el potencial es mínimo.

Los puntos del plano x,y, respresentan la distancia del punto real al cuerpo generador de campo y sobre el eje z se representa el valor concreto del potencial gravitatorio para esa distancia r.

Para distancias muy próximas al cuerpo,en la superficie del mismo, el potencial es mínimo.

Gráfica de intensidad de campo en función de la distancia

En esta gráfica se suele representar la distancia al origen ( r ) en el eje x y el valor o módulo de la intensidad del campo gravitatorio ( g ) en el eje y. Normalmente la encontrarás asociada a la intensidad de campo producida por una partícula puntual o por un cuerpo esférico de masa M. Recuerda que el valor de la intensidad de campo gravitatorio a una determinada distancia r en el exterior de un cuerpo esférico homogéneo o de una partícula puntual de masa M viene dado por la expresión: g(r)=G⋅Mr2 . Recuerda también que, si la esfera es hueca, el campo en el interior es 0. Y si es sólida tiene un crecimiento lineal de la forma: g(r)=G⋅MResfera3⋅r . De esta forma podemos encontrarnos con las siguientes gráficas:

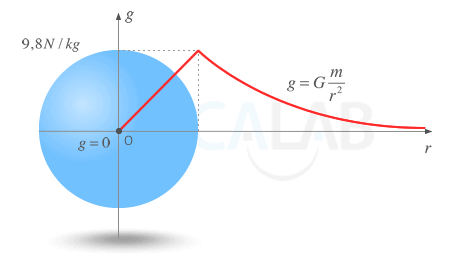
Módulo de la intensidad de campo creado por una esfera sólida

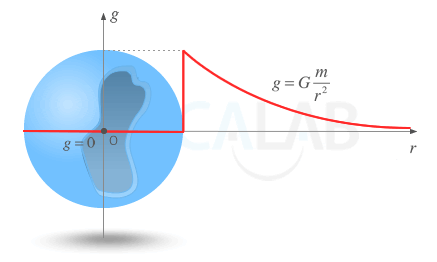
Módulo de la intensidad de campo creado por una cáscara esférica