DIOPTRIO ESFÉRICO

Se denomina dioptrio esférico a cualquier superficie esférica que separa dos medios transparentes de distinto índice de refracción.

 Aproximación paraxial En el estudio de la formación de imágenes nos vamos a limitar a los rayos paraxiales, que son aquellos que forman ángulos muy pequeños con el eje, menores de 10º , separándose muy poco de él a través de todo su recorrido de objeto a imagen.

Esta aproximación nos permite utilizar la siguiente aproximación, sin que el error cometido sea significativo: a ≅ sen a  ≅ tg a. Donde el ángulo se expresa en radianes.

Observa, como ejemplo, que para un ángulo de 5º : tg 5º = 0,0875 ; y que 5º son 0,0873 rad.


Tenemos un casquete esférico de radio r = BC y vértice O que separa dos medios de índices de refracción n e n', siendo n' > n

Un punto luminoso A situado sobre el eje óptico emite un rayo AP hacia el dioptrio. Este rayo forma un ángulo a con el eje y se refracta siguiendo el camino PA' formando un ángulo a' con el eje óptico.

Como n' > n el rayo refractado se aproxima a la normal y a ' < a

El rayo AO coincide con la normal, es perpendicular al dioptrio y no se desvía al incidir sobre él. Este rayo corta al rayo PA' en el punto A'. Este punto A' es la imagen de A.

Los rayos son paraxiales, y están muy próximos al eje óptico de manera que OB es una distancia casi cero y PB es muy pequeña. Estas distancias son despreciables si se comparan con s, s' y con r. En esta zona paraxial los senos de los ángulos y las tangentes coinciden pudiendo sustituirse por los valores de los propios ángulos expresados en radianes.

Aplicando la ley de Snell para la refracción:

n sen e = n' sen e'

n · e = n'· e'

Expresando los ángulos en valor absoluto en el triángulo PCA' podemos deducir que:

 |a' |+ |e '| + |p '| =180 º (suma de los ángulos internos de un triángulo)

|b'| +| p '| = 180 º 

Igualando las expresiones anteriores:   |a'| + |e '| = |b'|

Aplicando criterios DIN y como los tres ángulos son positivos:

a' + e' = b'    y en consecuencia   e' = b' -a' 

En el triángulo APC podemos deducir que:

 |a| + |p| + |b'| =180º

|e| + |p| =180º

Igualando las expresiones anteriores:    |a| + |b'| = |e |

Aplicando criterios DIN y siendo:   - a + b' = e

Aplicando la ley de Snell:   n · e = n'· e'

n (- a+ b' )= n'(b' -a' )

En la figura podemos establecer las relaciones siguientes:

tg a = h /s = a     tg b'= h/r= b'     tg a'= h/s' = a'

Substituyendo en la Ley de Snell:

Esta expresión se llama Invariante de Abbe (en honor de Emst Abbe). El valor de la expresión es igual tanto si se escribe en el espacio objeto como si se hace en el espacio imagen.

Esta es la ecuación fundamental del dioptrio esférico.

Permite conocer la posición de la imagen si previamente conocemos la posición del objeto y las características del dioptrio. Solamente es válida para los rayos paraxiales.

Todos los rayos que salen de A son paraxiales (se separan poco del eje principal) y convegen en el punto A'.

El sistema óptico que cumple esta condición recibe el nombre de estigmático.

Focos y distancias focales

Existen dos puntos muy importantes cuando estudiamos un dioptrio: su foco objeto y su foco imagen.

El foco objeto de un dioptrio esférico es el punto F del eje óptico en el que tendría que situarse un objeto para que sus rayos saliesen paralelos al eje tras refractarse en el dioptrio. La distancia del foco objeto al vértice del dioptrio se denomina distancia focal objeto y se denota por f. Se cumple que:

f=−R⋅nn'−n

Donde la unidad de medida en el Sistema Internacional (S.I.) de f es el metro ( m ) y el resto de magnitudes ya han sido presentadas anteriormente.

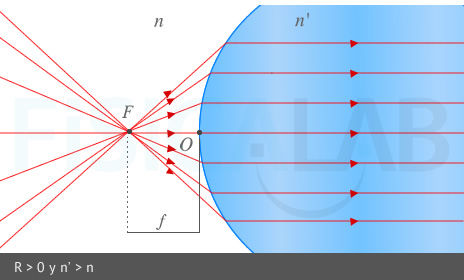
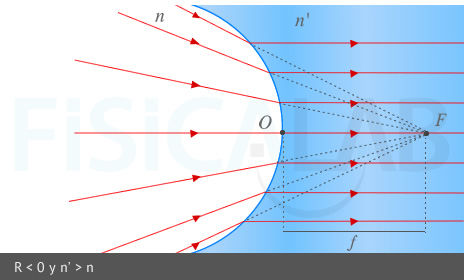
Foco objeto y distancia focal objeto.

Los rayos que pasan por el foco F, a una distancia f del vértice u origen O del diptrio, salen paralelos al eje óptico tras refractarse en este. En la primera imagen tenemos un dioptrio esférico convexo (R > 0) ⇒ f < 0 (lado izquierdo del dioptrio). En la segunda imagen tenemos un dioptrio esférico cóncavo (R < 0 ) ⇒ f > 0 (lado derecho del dioptrio)

El foco imagen de un dioptrio esférico es el punto F' del eje óptico en el que convergen, tras pasar por el dioptrio, los rayos que son paralelos al eje óptico. La distancia del foco imagen al vértice del dioptrio se denomina distancia focal imagen y se denota por f'. Se cumple que:

f'=R⋅n'n'−n

Donde la unidad de medida en el Sistema Internacional (S.I.) de f' es el metro ( m ) y el resto de magnitudes ya han sido presentadas anteriormente.

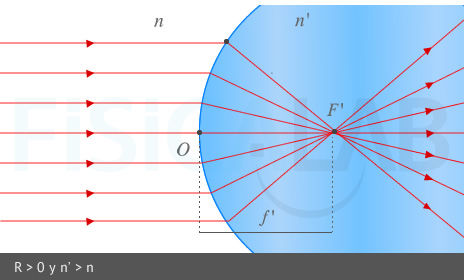
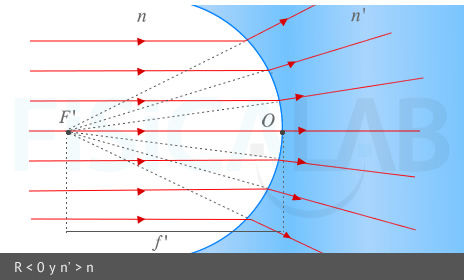
Foco imagen y distancia focal imagen.

Los rayos provenientes del infinito, paralelos al eje óptico, convergen todos en el foco F', a una distancia f' del vértice u origen O del diptrio, tras refractarse en este. En la imagen superior tenemos un dioptrio esférico convexo (R > 0) ⇒ f' > 0 (lado derecho del dioptrio). En la imagen izquierda tenemos un dioptrio esférico cóncavo (R < 0 ) ⇒ f'<0 (lado izquierdo del dioptrio)

Puesto que f y f' son distancias, seguimos para ellas el mismo criterio de signos que para s y s' respectivamente.

¡Atención! La expresión para la distancia focal objeto presupone el criterio de signos DIN. Es habitual que encuentras también la siguiente:

f=R⋅nn'−n

Esta última expresión asume el segundo criterio de signos que te presentamos, en el que f debe ser positivo para los objetos reales, es decir, situados delante del dioptrio, y el resto de magnitudes coinciden en signo. Por contra, la expresión de la distancia focal imagen es válida para cualquiera de los dos convenios de signos presentados en el tema.

Características

Las dos expresiones presentadas nos permiten llegar a algunas relaciones interesantes:

• Si dividimos f entre f':
  ff'=nn'
  
  
  En donde se observa que las distancias focales son directamente proporcionales a sus respectivos índices de refracción. También puedes deducir que la distancia focal es mayor, en valor absoluto, en el medio que tenga mayor índice de refracción
• Si sumamos f con f' :
  f+f'=R
  
  
  Es decir, la suma de las distancias focales es igual al radio de curvatura
• Si dividimos los dos miembros de la ecuación fundamental del dioptrio esférico entre el segundo, obtenemos la ecuación de Gauss:
  f's'+fs=1

Comprobaciones

Aunque hasta ahora hemos presentado muchas fórmulas distintas, lo cierto es que todas parten de la ecuación fundamental. Así, podemos deducir la ecuación de la distancia focal objeto recordando que los rayos deben salir paralelos al eje óptico, lo que significa que s'=∞. Para ese valor de s', s=f , con lo que:

n'∞−nf=n'−nR⇒f=−R⋅nn'−n

Por otro lado, podemos deducir la ecuación de la distancia focal imagen recordando lo qué significa que los rayos incidan paralelos al eje óptico, que s=-∞. Para ese valor de s, s'=f' , con lo que:

n'f'−n−∞=n'−nR⇒f'=R⋅n'n'−n